ESTUDANDO EM CASA: POTENCIAÇÃO

O Profº Caju tem um site para vestibulares, mas explica tão claramente
esta matéria, que qualquer adolescente poderá entendê-la, se você duvida, veja abaixo e depois se quiser visite o site (clique em estude on line)

http://www.tutorbrasil.com.br
Em tempo: A explicação da fatoração em números primos
também é do Profº Caju,
veja na postagem Números Primos - M.D.C. e M.M.C.

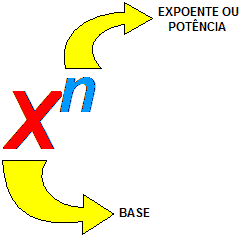
Para indicar que um número está elevado à uma potencia qualquer, colocamos esta potência como expoente. Veja o exemplo.

5 elevado à potência 4
5⁴

Quando dizemos que um número qualquer está "elevado à potencia 4", por exemplo, estamos dizendo que este número será multiplicado por ele mesmo 4 vezes. Vamos desenvolver o exemplo acima:

5⁴= 5 · 5 · 5 · 5 = 625

Veja mais exemplos:

2⁹= 2 · 2 · 2 · 2 · 2 · 2 · 2 · 2 · 2 = 512
3³ = 3 · 3 · 3 = 27
8²= 8 · 8 = 64

Genericamente podemos representar uma potência:

Onde chamamos "X" de base e "n" de "expoente" ou "potência".
Com esta definição de potenciação, podemos efetuar algumas continhas utilizando estas potências. Por exemplo, podemos multiplicar 5³ por 5⁹.
Veja abaixo como fazer isso...

MULTIPLICAÇÃO DE POTÊNCIAS DE MESMA BASE

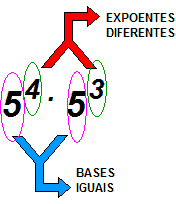Esta é a primeira propriedade pois é a mais utilizada de todas.
Por exemplo, se aparecer o número 5⁴ multiplicado por 5³,

Esta é a operação que queremos efetuar. Vamos abrir a potência

$formdata=(5\,\cdot\,5\,\cdot\,5\,\cdot\,5)\,\cdot\,(5\,\cdot\,5\,\cdot\,5)$

Agora veja que esta multiplicação é igual à 5 elevado à potência sete. Este 7 veio da soma dos 4 fatores de 5⁴ com os 3 fatores de 5³

Daqui nós tiramos a regra para qualquer multiplicação de potências com mesma base.
Conserva-se a base e soma-se o expoente. Genericamente temos:

Esta é a regra. "X" pode ser qualquer número (real, imaginário...), que a regra continuará valendo.
Conserva-se a base e soma-se os expoentes.
É muito importante entendê-la, pois é muito utilizada.
Note que a base deve ser a mesma nos fatores, e ela que aparecerá no produto.

DIVISÃO DE POTÊNCIAS DE MESMA BASE

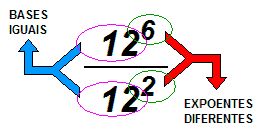O mesmo raciocínio mostrado para a multiplicação, pode ser aplicado para a divisão.
O exemplo será 12⁶ divididos por 12²

$formdata=\Large\frac{12^6}{12^2}$

Esta é a divisão que queremos efetuar. Vamos novamente abrir a potência.

$formdata=\Large\frac{12\,\cdot\,12\,\cdot\,12\,\cdot\,12\,\cdot\,12\,\cdot\,12}{12\,\cdot\,12}$

Agora podemos cortar os termos semelhantes que estão acima e abaixo da fração.
Portanto podemos cortar dois fatores 12 de cima com dois fatores 12 de baixo.

Ao cortar, estaremos retirando 2 unidades da potência de cima. Estas duas unidades são referentes ao expoente 2 da potência de baixo.

$formdata=12\,\cdot\,12\,\cdot\,12\,\cdot\,12=12^4$

$formdata=\fra{12^6}{12^2}=12^{6-2}=12^4$

Veja que esta multiplicação é igual à 12⁴ , isto nos dá a regra para qualquer divisão de potências com mesma base.
Conserva-se a base e subtrai-se os expoentes.
Genericamente, temos:

Novamente, "X" pode ser qualquer número (real, imaginário...) que a regra ainda vale. Estas são as duas regras mais utilizadas.

MULTIPLICAÇÃO DE POTÊNCIAS DE MESMO EXPOENTE

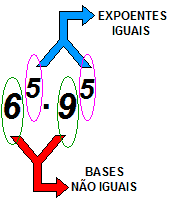Até agora vimos multiplicação e divisão com termos de mesma base. E quando não tiver mesma base??? O que podemos fazer?
Só podemos efetuar uma operação quando tivermos mesma base ou mesmo expoente. O que vamos ver agora é justamente o segundo caso: expoentes iguais.
O exemplo será 6⁵multiplicados por 9⁵:

$formdata=6^5\cdot+9^5$

Este é o exemplo. Agora vamos abrir as potências.

$formdata=6\cdot+6\cdot+6\cdot+6\cdot+6\cdot+9\cdot+9\cdot+9\cdot+9\cdot+9$

Qualquer multiplicação tem a propriedade de comutatividade, ou seja, se invertermos a ordem de multiplicação o valor não se altera. Então vamos colocar esta multiplicação em outra ordem.

$formdata=6\cdot+9\cdot+6\cdot+9\cdot+6\cdot+9\cdot+6\cdot+9\cdot+6\cdot+9$
$formdata=(6\cdot+9)\cdot(6\cdot+9)\cdot(6\cdot+9)\cdot(6\cdot+9)\cdot(6\cdot+9)$

Agora temos a multiplicação 6 · 9 aparecendo 5 vezes. Então

$formdata=6^5\cdot+9^5=(6\cdot+9)^5$

E esta propriedade podemos aplicar para qualquer número.
Conserva-se o expoente e multiplica-se a base.
Generalizando:

Os números "X" e "Y" podem ser quaisquer números do conjunto dos complexos.

DIVISÃO DE POTÊNCIAS DE MESMO EXPOENTE

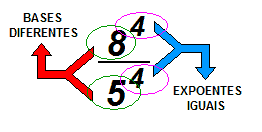O mesmo raciocínio mostrado para a multiplicação, pode ser aplicado para a divisão.
O exemplo será 8⁴ divididos por 5⁴:

$formdata=\frac{8^4}{5^4}$

Este é o exemplo que iremos usar. Vamos abrir as potências.

$formdata=\frac{8\,\cdot\,8\,\cdot\,8\,\cdot\,8}{5\,\cdot\,5\,\cdot\,5\,\cdot\,5}$

Como temos multiplicação em cima e em baixo da fração, podemos separar em 4 frações multiplicadas uma pela outra.

$formdata=\frac+85\,\cdot\,\frac+85\,\cdot\,\frac+85\,\cdot\,\frac+85$

E isto é a fração $formdata=\frac+85$ elevado na potência 4.

$formdata=\frac{8^4}{5^4}=\left(\frac+85\right)^4$

E esta propriedade pode se aplicar para quaisquer números do conjunto dos complexos. Generalizando,

Os números "X" e "Y" podem ser quaisquer números do conjunto dos números complexos.
Conserva-se o expoente e divide-se as bases.

POTÊNCIA DE POTÊNCIA

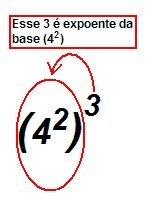Já vimos as principais propriedades de operações.
Agora vamos ver quando tivermos uma potência de um número que já tem uma potência. Veja o exemplo:

(4²)³

O que devemos fazer?
Vamos desenvolver este exemplo:

$formdata=(4^2)^3$

Vamos abrir a potência de dentro do parênteses

$formdata=(4\cdot+4)^3$

Agora a potência fora do parênteses diz que devemos multiplicar o que tem dentro do parênteses três vezes,

$formdata=(4\cdot+4)\cdot+(4\cdot+4)\cdot+(4\cdot+4)$

$formdata=4\cdot+4\cdot+4\cdot+4\cdot+4\cdot+4$

E isso nos dá a potência 4⁶. E agora tiramos outra regra para potências.

Generalizando, ficamos com:

Onde "a" e "b" podem ser quaisquer números do conjunto dos complexos.
Potência de potência, multiplica-se os expoentes.

ATENÇÃO

Quando tivermos um número negativo elevado numa potência, devemos tomar a seguinte precaução, veja os exemplo:

(-5)² = (-5) · (-5) = +25

(-2)⁴= (-2) · (-2) · (-2) · (-2) = +16

Note, então, que quando temos um número negativo elevado em qualquer expoente PAR este se comporta como se fosse positivo, pois na multiplicação "menos com menos dá mais":

(-5)²=5²=25

(-2)⁴=2⁴=16

Se "k" for PAR (-X)^k=X^k

E se tivermos um expoente ímpar?

(-5)³=(-5)·(-5)·(-5)	Se pegarmos os dois primeiro números multiplicados, temos (-5)²=+25, substituindo ao lado:
(-5)³=25·(-5)=-125	Sempre que tivermos um número negativo elevado em qualquer expoente ÍMPAR, o sinal negativo permanece na resposta

PEGA-RATÃO

(-5)² é totalmente diferente de -5² . No primeiro caso o sinal de menos também está elevado ao quadrado, então a resposta é +25. Já no segundo caso, o menos não está elevado ao quadrado, somente o 5, portanto a resposta é -25.

Com base nas operações com potências, existem algumas propriedades interessantes de serem vistas.

$formdata=\Large{a^0}=1$

Qualquer número elevado à potência ZERO resulta 1.
Só não pode ser 0⁰, pois este não existe!

Ex.:	$formdata=2^0=1$	$formdata=(-2,3)^0=1$
	$formdata=\left(\frac{27}{32}\right)^0=1$	$formdata=\left(\sqrt[4]{37}\right)^0=1$

$formdata=\Large{a^1}=a$

A potência 1 indica que devemos multiplicar "a" por ele mesmo 1 única vez. Portanto, é o próprio "a".

Ex.:	$formdata=23^1=23$	$formdata=(-234)^1=-234$
	$formdata=(\sqrt{34})^1=\sqrt{34}$	$formdata=\left(-\frac{2}{37}\right)^1=-\frac{2}{37}$

$formdata=\Large{1^n}=1$

A potência "n" indica quantas vezes o número 1 será multiplicado por ele mesmo, e não interessa quantas vezes seja, sempre será 1.

Ex.:	$formdata=1^4=1$	$formdata=1^{\frac{2}{3}}=1$
	$formdata=1^{(-47)}=1$	$formdata=1^{\sqrt+5}=1$

$formdata=\Large{0^n}=0$

Idem ao de cima. Não interessa quantas vezes o zero seja multiplicado por ele mesmo, sempre será zero.
Lembre-se que não pode ser 0⁰, pois não existe!

Ex.:	$formdata=0^2=0$	$formdata=0^{-21}=0$
	$formdata=0^{(2.3)}=0$	$formdata=0^{\frac{5}{6}}=0$

$formdata=\Large+a^{-n}=\frac{1}{a^n}$

Sempre que tivermos um expoente negativo, este troca de numerador para denominador, ou seja, vai de cima da fração para de baixo da fração.

Ex.:	$formdata=3^{-2}=\frac{1}{3^2}$	$formdata=7^{-\frac{5}{3}}=\frac{1}{7^{\frac{5}{3}}}$
	$formdata=\left(\frac{2}{9}\right)^{-4}=\left(\frac{9}{2}\right)^{4}=$	$formdata=(\sqrt+7)^{-2}=\frac{1}{(sqrt+7)^2}$

$formdata=\Large\frac{1}{a^{-n}}=a^n$

A regra acima também vale ao contrário. Se tivermos uma potência negativa no denominador, este se transforma em numerador ao trocar o sinal da potência.