OPERAÇÕES COM NÚMEROS INTEIROS

SUBTRAÇÃO:
As operações de subtração envolvendo os números Inteiros requerem algumas situações teóricas que relacionam os possíveis sinais operatórios. 
Regras operatórias:Sinais iguais: soma e conserva o sinal.
Sinais diferentes: subtrai e conserva o sinal do maior módulo.
Operações sem parênteses
+ 10 – 7 = + 3 (Sinais diferentes: subtrai e conserva o sinal do maior módulo)– 3 – 3 = – 6 (Sinais iguais: soma e conserva o sinal)+ 20 – 30 = – 10 (Sinais diferentes: subtrai e conserva o sinal do maior módulo)– 12 + 3 = – 9 (Sinais diferentes: subtrai e conserva o sinal do maior módulo)– 9 + 9 = 0 (operação entre números opostos, resultado sempre será 0)– 25 + 24 = – 1 (Sinais diferentes: subtrai e conserva o sinal do maior módulo)
Operações com parênteses
Nesse caso, as operações de subtração podem ser resolvidas eliminando os parênteses, isso será feito aplicando algumas regras que envolvem jogo de sinal, observe:

+ (+) = +

+ (–) = –

– (+) = –

– (–) = +

Eliminado os parênteses, passa a valer as regras operatórias:
(+10) – (–23) = +10 + 23 = + 33
(+20) – (+12) = +20 – 12 = + 8
(–32) + (–5) = – 32 – 5 = – 37
(–27) – (–30) = –27 + 30 = + 3


SOMA:
Na soma de dois números inteiros com sinais iguais, o valor absoluto será a soma das parcelas, e o sinal será o mesmo das parcelas.Exemplo: (+ 5) + (+ 4) = + 9
(- 5) + (- 4) = - 9

Na soma de dois números inteiros com sinais diferentes, o valor absoluto será a diferença das parcelas e o sinal será o da parcela de maior valor absoluto.Exemplo: (- 5) + (+ 4) = - 1

A Soma de dois números inteiros opostos é ZERO.Exemplo: (+ 10) + (- 10) = 0
Simplificando a escrita:

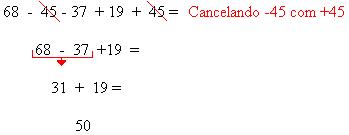MULTIPLICAÇÃO:
O conjunto dos números inteiros é formado pelos números inteiros positivos e seus respectivos negativos, denominado oposto ou simétrico. A multiplicação entre esses números deverá respeitar algumas regras envolvendo jogo de sinais.

Produto de dois números inteiros com sinais diferentes.
Quando realizamos a multiplicação:
5 x 6 é o mesmo que 6 + 6 + 6 + 6+ 6. Então, para multiplicarmos dois números inteiros com sinais diferentes, iremos utilizar a mesma ideia.
(+5) * (– 2)
(– 2) + (– 2) + (– 2) + (– 2) + (– 2) (Escrevendo uma adição de parcelas iguais)
– 2 – 2 – 2 – 2 – 2 = – 10 (Simplificando a escrita e calculando o resultado)
(+5) * (– 2) = –10O produto de dois números inteiros, diferente de zero, e de sinais diferentes é um número inteiro de valor absoluto igual ao produto dos valores absolutos dos fatores e sinal negativo (–).

Produto de dois números inteiros com sinais iguais.
Nesse caso há duas possibilidades: dos fatores serem positivos ou dos fatores serem negativos.
Vamos calcular o produto de (+ 8) * (+5) = + 40
Vamos calcular o produto de (– 6) * (– 15) = + 90O produto de dois números inteiros diferentes de zero e de sinais iguais é um número inteiro devalor absoluto igual ao produto dos valores absolutos dos fatores e sinal positivo (+).

A multiplicação dos números inteiros é mais simples que a adição e subtração, pois basta multiplicarmos os valores absolutos e o sinal fica conforme a regra:

( + ) * ( + ) = ( + )

( + ) * ( – ) = ( – )

( – ) * ( + ) = ( – )

( – ) * ( – ) = ( + )

DIVISÃO:

Segundo o dicionário Aurélio, divisão significa “partir ou distinguir em diversas partes; separar as diversas partes de.”
Na divisão utilizamos praticamente o mesmo método da multiplicação. Devemos, em primeiro lugar, relembramos o jogo de sinais:
- Divisão de números com mesmo sinal = +
- Divisão de números com sinais diferentes = -

Numa divisão exata de dois números inteiros, o quociente é um número inteiro e o resto é igual a zero.



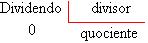
►Quociente de dois números inteiros com sinais diferentes.
(- 45) : (+ 5) = - 9
(+45) : ( -5) = -9

O quociente de uma divisão exata entre dois números inteiros, com divisor diferente de zero e sinais diferentes é um número inteiro de:
Valor absoluto: igual ao quociente dos valores absolutos dos termos.
Sinal: negativo (-).

►Quociente de dois números inteiros com sinais iguais.

(- 60) : (- 10) = + 6
(+ 60) : (+ 10) = + 6

O quociente de uma divisão exata entre dois números inteiros, com divisordiferente de zero e sinais iguais é um número inteiro de:
Valor absoluto: igual ao quociente dos valores absolutos dos termos.
Sinal: positivo (+).

Acontece da mesma forma que na multiplicação, dividimos os valores absolutos e o sinal é conforme a regra:
- : + = -
+ : + = +
- : - = +

Observações:
• Não existe divisão por zero. Exemplo: 15 : 0, pois não existe um número inteiro cujo produto por zero seja 15.

• Zero dividido por qualquer número é sempre zero.

O conteúdo desta postagem foi retirado do 

blog do 

PROF° ANTONIO CARNEIRO

http://ensinodematemtica.blogspot.com.br/